時間複雜度 Time Complexity
| 操作 | Time Complexity 時間複雜度 |
|---|---|
| Lookup | O(n) |
| Insert | O(log N) |
| Delete | O(log N) |
Min Heap 最小堆積
完全二元樹所有
父節點都比子節點要小,就屬於最小堆積
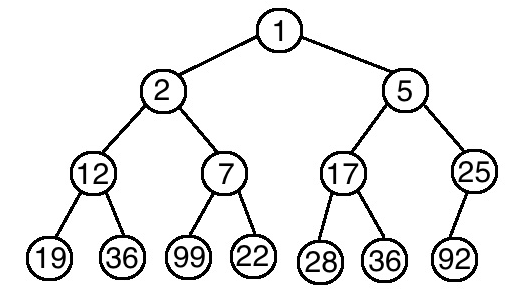
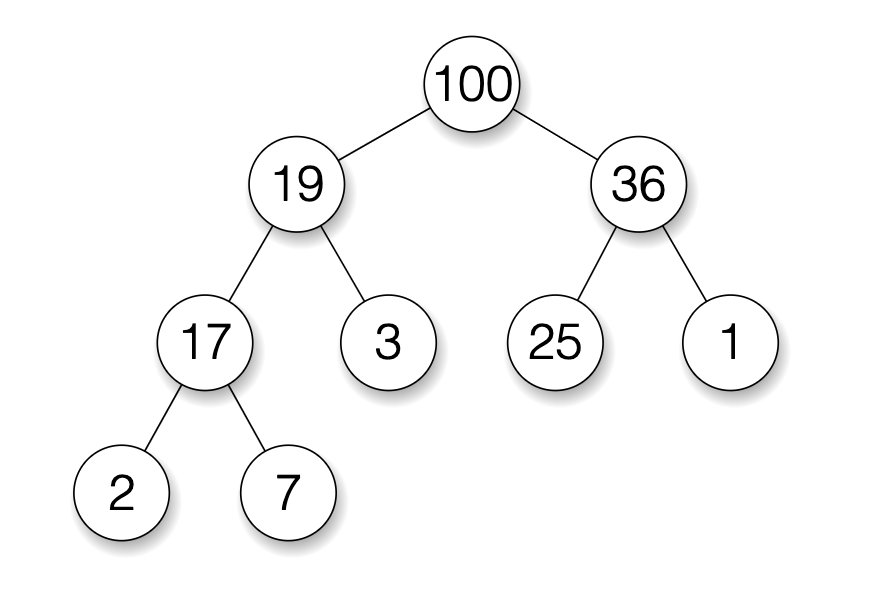
Max Heap 最小堆積
完全二元樹所有
父節點都比子節點要大,就屬於最大堆積
- Binary Heap 和記憶體中的 Heap 沒有關係
- Parent 的數值一定大於 Child
- Binary Heap 中 parent node 的數值,一定大於 child node 的數值。
- root 會是所有 Node 中的最大值。
- Binary Heap 很常被使用在 Priority Queue。
時間複雜度 Time Complexity
| 操作 | Time Complexity 時間複雜度 |
|---|---|
| Lookup | O(n) |
| Insert | O(log N) |
| Delete | O(log N) |
Heap 結構
- 由上到下
- 由左到右
陣列索引順序
陣列 [10, 6, 7, 5, 15, 17, 12] 會依序在 Heap 樹 由上到下及由左到右放置
10
/ \
6 7
/ \ / \
5 15 17 12
| 陣列 | 10 | 6 | 7 | 5 | 15 | 17 | 12 |
|---|---|---|---|---|---|---|---|
| 索引位置 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
陣列數字演算法
| 節點 | 演算法 |
|---|---|
| parent 母節點 | (currentNumberIndex -1) / 2 |
| left child 左節點 | 2 * currentNumberIndex + 1 |
| right child 右節點 | 2 * currentNumberIndex + 2 |
計算 [10, 6, 7, 5, 15, 17, 12] 陣列中數字 6 的節點
10
/ \
6 7
/ \ / \
5 15 17 12
- 6 的索引位置:1
| 節點 | 演算法 | 母節點索引位置 | 母節點索引位置數字 |
|---|---|---|---|
| parent 母節點 | (1 - 1) / 2 |
0 | 10 |
| left child 左節點 | 2 * 1 + 1 |
3 | 5 |
| right child 右節點 | 2 * 1 + 2 |
4 | 15 |
計算 [10, 6, 7, 5, 15, 17, 12] 陣列中數字 7 的節點
10
/ \
6 7
/ \ / \
5 15 17 12
- 7 的索引位置:2
| 節點 | 演算法 | 母節點索引位置 | 母節點索引位置數字 |
|---|---|---|---|
| parent 母節點 | (2 - 1) / 2 |
0 | 10 |
| left child 左節點 | 2 * 2 + 1 |
5 | 17 |
| right child 右節點 | 2 * 2 + 2 |
6 | 12 |
Max Heap 比較流程
1. 從中間點找最大值
比較左右節點,確認是否有彼此節點大的數字,如果有的話則將此節點交換往上移動
中間節點:Math.floor(整數長度 / 2) = 7/2 = 3.5 = 3
10
/ \
6 7
/ \ / \
5 15 17 12
- 索引 3 數字 5
| 節點 | 演算法 | 母節點索引位置 | 母節點索引位置數字 |
|---|---|---|---|
| left child 左節點 | 2 * 3 + 1 |
7 | 找不到 |
| right child 右節點 | 2 * 3 + 2 |
8 | 找不到 |
確認中間節點的左右節點,都比中間節點 數字 5 較小
而因為找不到 數字 5 的左右節點,所以確認 數字 5 是這三個節點中最大
2. 往中間點左方移動,繼續找最大值
索引 3 數字 5的左方是索引 2 數字 7
10
/ \
6 7
/ \ / \
5 15 17 12
| 節點 | 演算法 | 母節點索引位置 | 母節點索引位置數字 |
|---|---|---|---|
| left child 左節點 | 2 * 2 + 1 |
5 | 17 |
| right child 右節點 | 2 * 2 + 2 |
6 | 12 |
這邊會找到左右節點比母節點還大,將最大的子節點移動到母節點,那這整棵 Heap 樹會變成
10
/ \
6 17
/ \ / \
5 15 7 12
整個陣列會從 [10, 6, 7, 5, 15, 17, 12] 變成 [10, 6, 17, 5, 15, 7, 12]
| 陣列 | 10 | 6 | 17 | 5 | 15 | 7 | 12 |
|---|---|---|---|---|---|---|---|
| 索引位置 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
3. 比較完成左方移動,繼續找最大值
索引 2 數字 17的左方是索引 1 數字 6
10
/ \
6 17
/ \ / \
5 15 7 12
| 節點 | 演算法 | 母節點索引位置 | 母節點索引位置數字 |
|---|---|---|---|
| left child 左節點 | 2 * 1 + 1 |
3 | 5 |
| right child 右節點 | 2 * 1 + 2 |
4 | 15 |
這邊會找到右節點比母節點還大,將最大的子節點移動到母節點,那這整棵 Heap 樹會變成
10
/ \
15 17
/ \ / \
5 6 7 12
整個陣列會從 [10, 6, 17, 5, 15, 7, 12] 變成 [10, 15, 17, 5, 6, 7, 12]
| 陣列 | 10 | 15 | 17 | 5 | 6 | 7 | 12 |
|---|---|---|---|---|---|---|---|
| 索引位置 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
4. 比較完成左方移動,繼續找最大值
索引 1 數字 15的左方是索引 0 數字 10
10
/ \
15 17
/ \ / \
5 6 7 12
| 節點 | 演算法 | 母節點索引位置 | 母節點索引位置數字 |
|---|---|---|---|
| left child 左節點 | 2 * 0 + 1 |
1 | 15 |
| right child 右節點 | 2 * 0 + 2 |
2 | 17 |
這邊會找到右節點比母節點還大,將最大的子節點移動到母節點,那這整棵 Heap 樹會變成
17
/ \
15 10
/ \ / \
5 6 7 12
整個陣列會從 [10, 15, 17, 5, 6, 7, 12] 變成 [17, 15, 10, 5, 6, 7, 12]
| 陣列 | 17 | 15 | 10 | 5 | 6 | 7 | 12 |
|---|---|---|---|---|---|---|---|
| 索引位置 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
5. 比較最後交換的數字
最後交換的數字是索引 2 數字 10
17
/ \
15 10
/ \ / \
5 6 7 12
| 節點 | 演算法 | 母節點索引位置 | 母節點索引位置數字 |
|---|---|---|---|
| left child 左節點 | 2 * 2 + 1 |
5 | 5 |
| right child 右節點 | 2 * 2 + 2 |
6 | 12 |
這邊會找到右節點比母節點還大,將最大的子節點移動到母節點,那這整棵 Heap 樹會變成
17
/ \
15 12
/ \ / \
5 6 7 10
整個陣列會從 [17, 15, 10, 5, 6, 7, 12] 變成 [17, 15, 12, 5, 6, 7, 10]
| 陣列 | 17 | 15 | 12 | 5 | 6 | 7 | 10 |
|---|---|---|---|---|---|---|---|
| 索引位置 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
參考資料
- Investigating Heap Sort - Why Is Heap Sort Θ(n * log(n))? An Even Longer Really Long Answer. - YouTube
- Implement A Binary Heap - An Efficient Implementation of The Priority Queue ADT (Abstract Data Type) - YouTube
- [資料結構] 堆積 (Heap) - iT 邦幫忙::一起幫忙解決難題,拯救 IT 人的一天
- [資料結構] Binary Heap | PJCHENder 未整理筆記
Donate KJ 贊助作者喝咖啡
如果這篇文章對你有幫助的話,可以透過下面支付方式贊助作者喝咖啡,如果有什麼建議或想說的話可以贊助並留言給我
If this article has been helpful to you, you can support the author by treating them to a coffee through the payment options below. If you have any suggestions or comments, feel free to sponsor and leave a message for me!
| 方式 Method | 贊助 Donate |
| PayPal | https://paypal.me/kejyun |
| 綠界 ECPay | https://p.ecpay.com.tw/AC218F1 |
| 歐付寶 OPay | https://payment.opay.tw/Broadcaster/Donate/BD2BD896029F2155041C8C8FAED3A6F8 |
