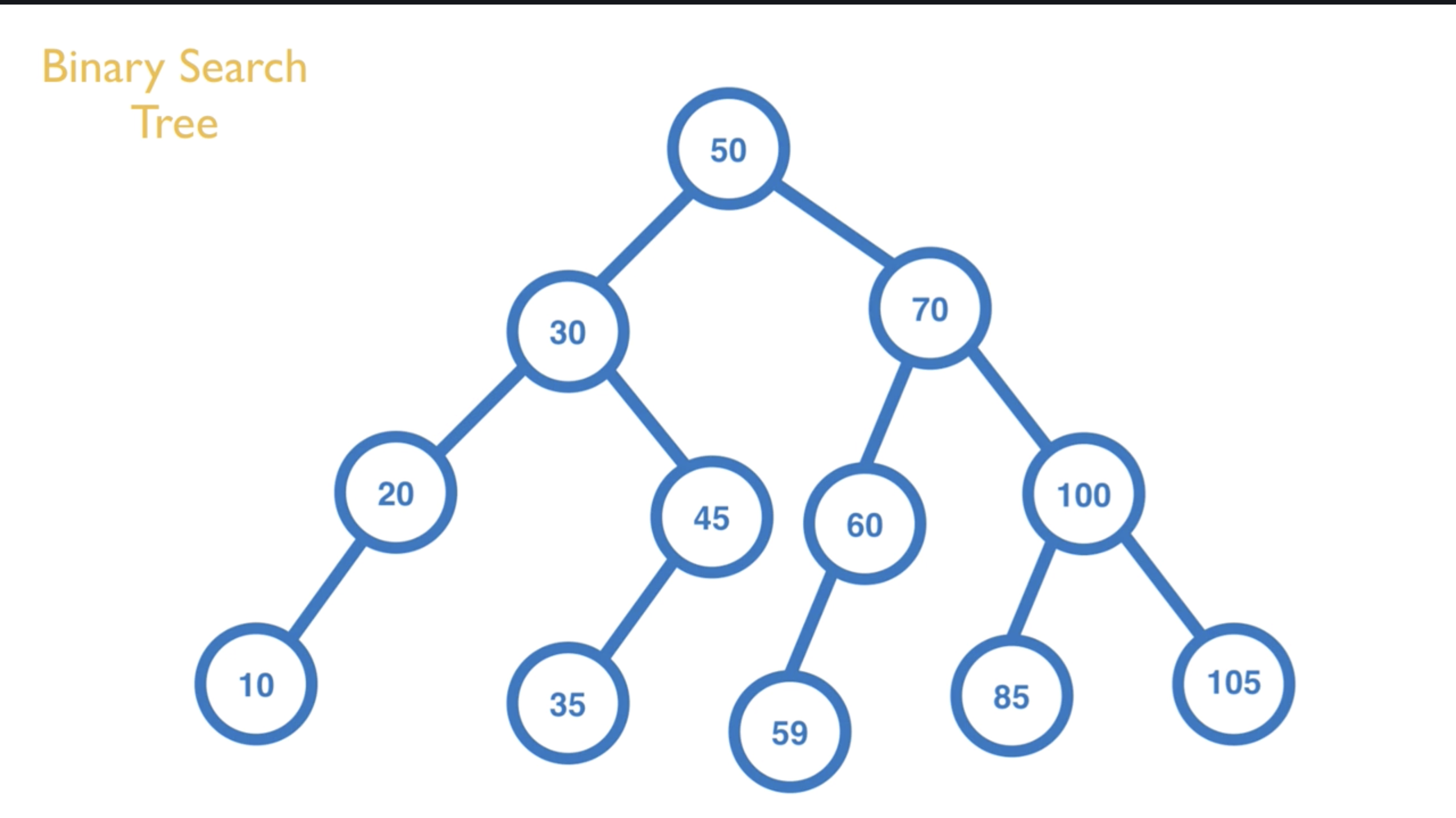
定義
- 每個 Node 會包含 value, left 和 right
- Binary Search Tree 會實作 lookup, insert, 和 remove 的方法
特性
- Perfect Binary Tree 有幾個重要的特性:
- 每下一層的 Node 數量都是上一層 Node 數的兩倍
- 最下層 Node 的數量會等於其上層所有 Node 數量加總後 + 1。例如,三層的 Perfect Tree,則三層 Node 的數量,會等同於前兩層的數量加總後再加 1,也就是 4 = 3 + 1。
- Node 的總數量會同於 2 的(Node 層數)次方 -1,也就是 2^h - 1
- Binary Search Tree 有一個很重要的概念是,它是有「階層(關係)」的概念在內,並不是把所有數字放在同一層排序。
時間複雜度 Time Complexity
| 操作 | Time Complexity 時間複雜度 |
|---|---|
| Lookup | O(log N) |
| Insert | O(log N) |
| Delete | O(log N) |
情境
但使用它有一個很重要的前提是資料必須盡量平均分散在左右兩邊,讓它長成一個樹狀結構,如果資料都是集中在某一側的話,則不適合使用 Binary Search Tree。
這種資料結構常用在「字典」、「電話簿」、「使用者資料」等等。
Depth First Traversal
- 由小到大依序迭代(in-order)
- 由上往下,由左至右(pre-order)
- 由下往上,由左至右(post-order)
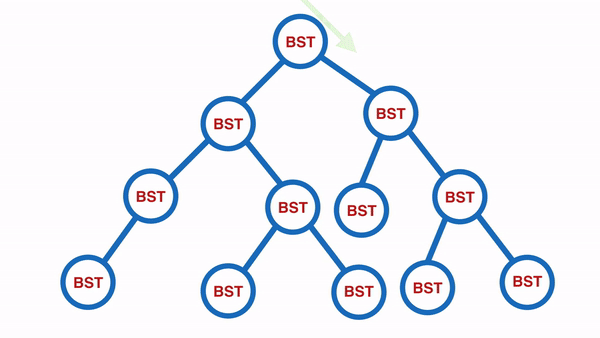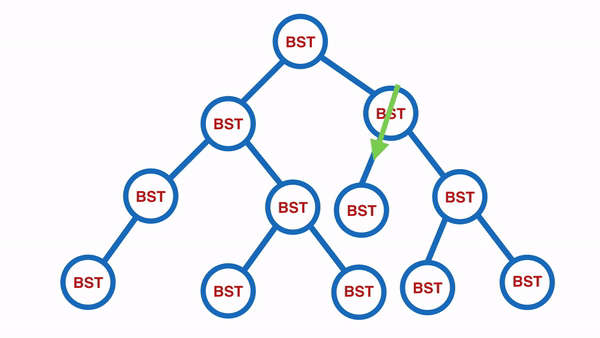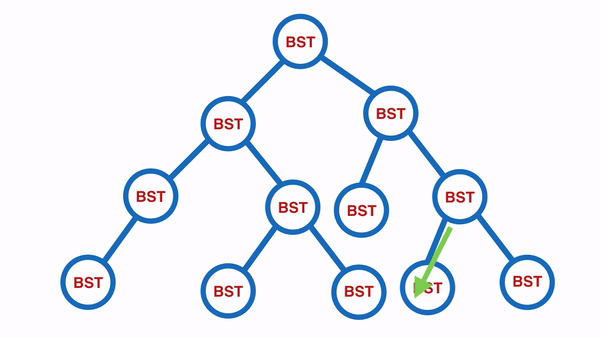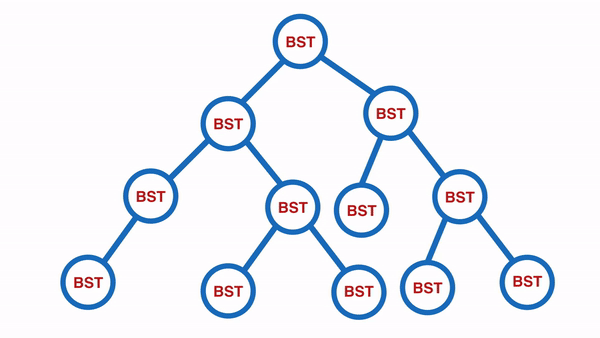
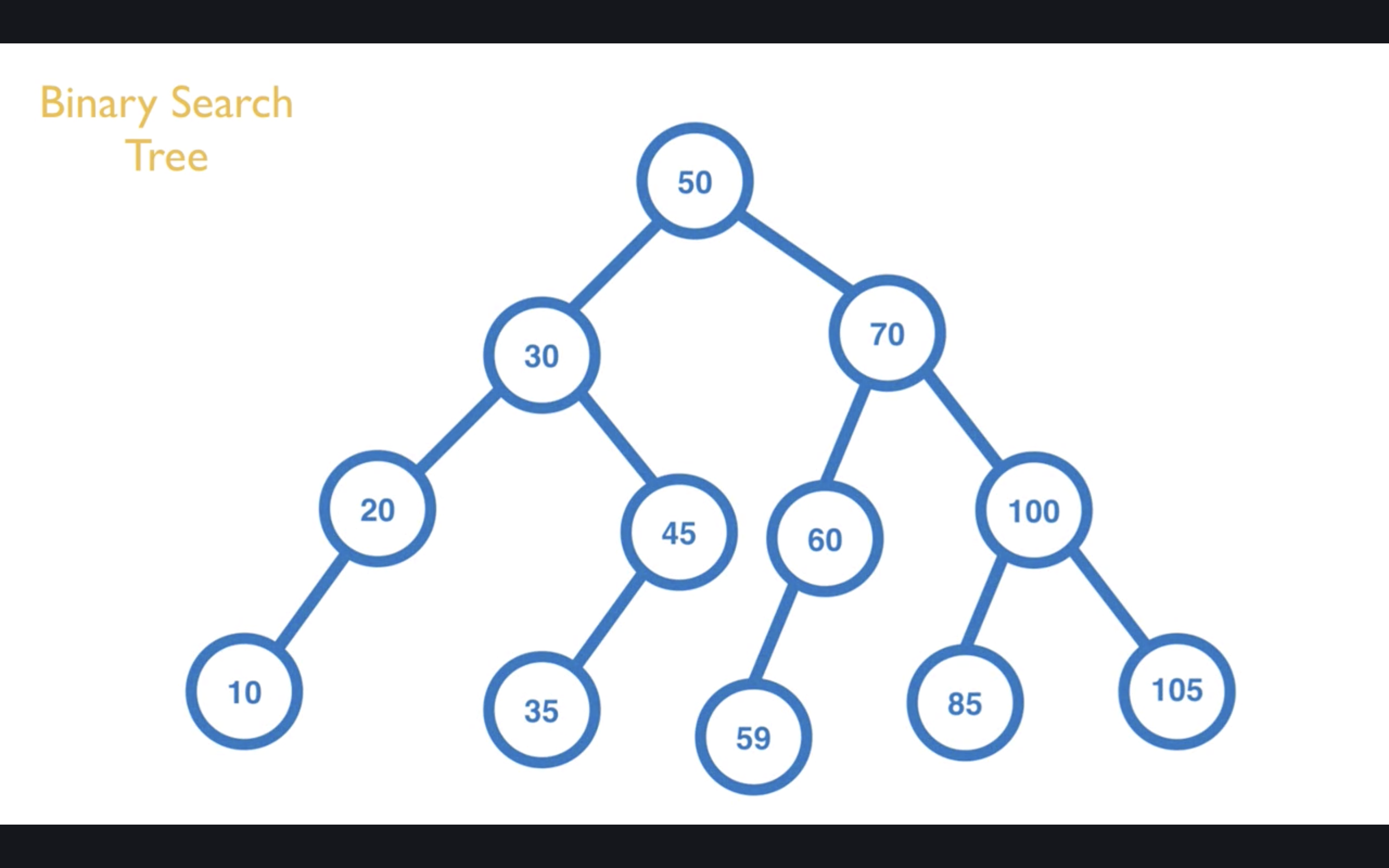
In-Order:由小到大依序迭代
從最底部開始,先把左邊的輸出,再輸出右邊的,如此所有的值就會由小到大依序排列。
輸出的內容會是:[10, 20, 30, 35, 45, 50, 59, 60, 70, 85, 100, 105]。
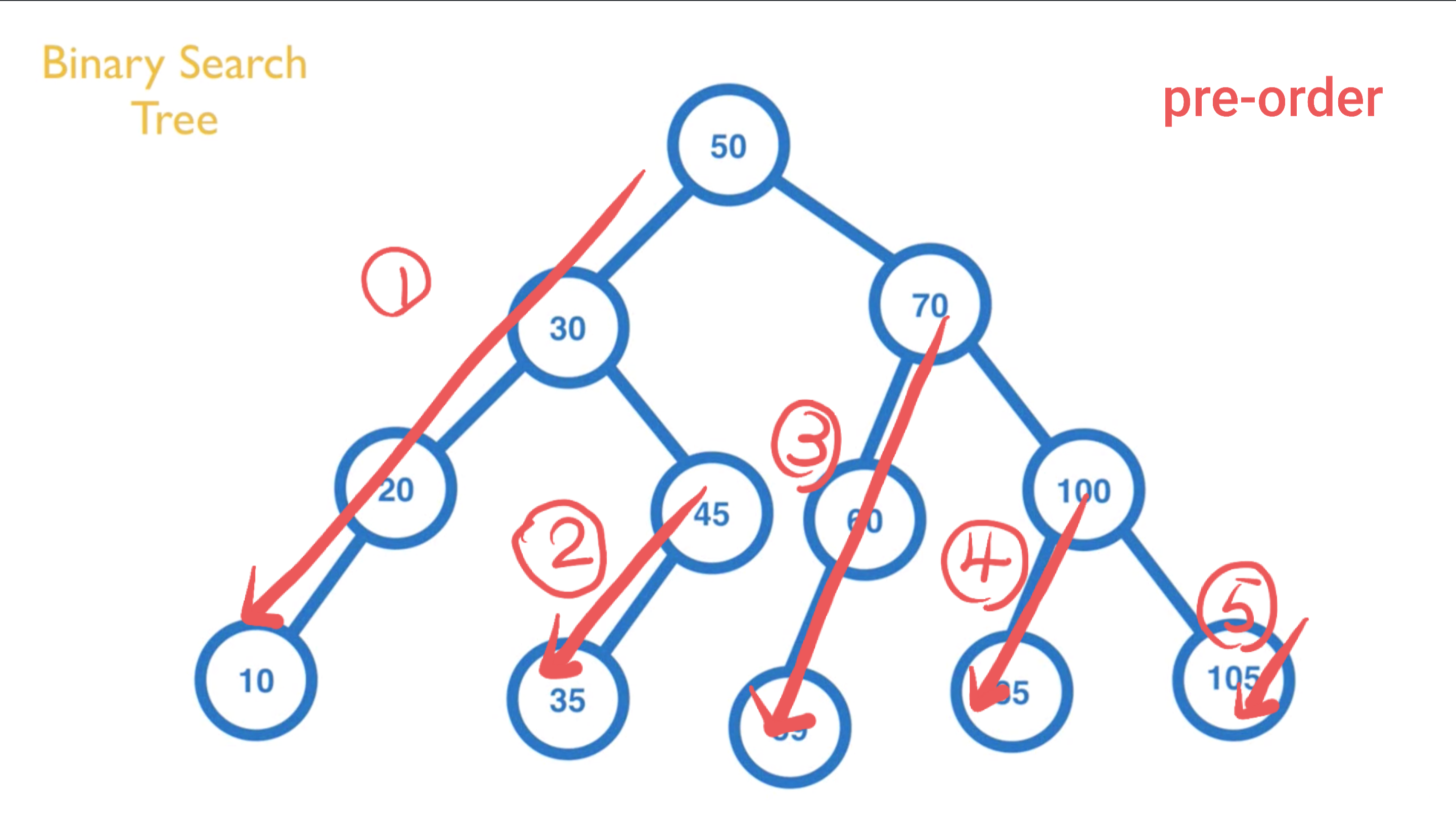
Pre-Order:由上往下,由左至右(中左右)
適合使用在想要 Copy Tree 時使用
由上往下,由左至右,依序輸出所有內容。
以下圖為例,會輸出 [50, 30, 20, 10, 45, 35, 70, 60, 59, 100, 85, 105]
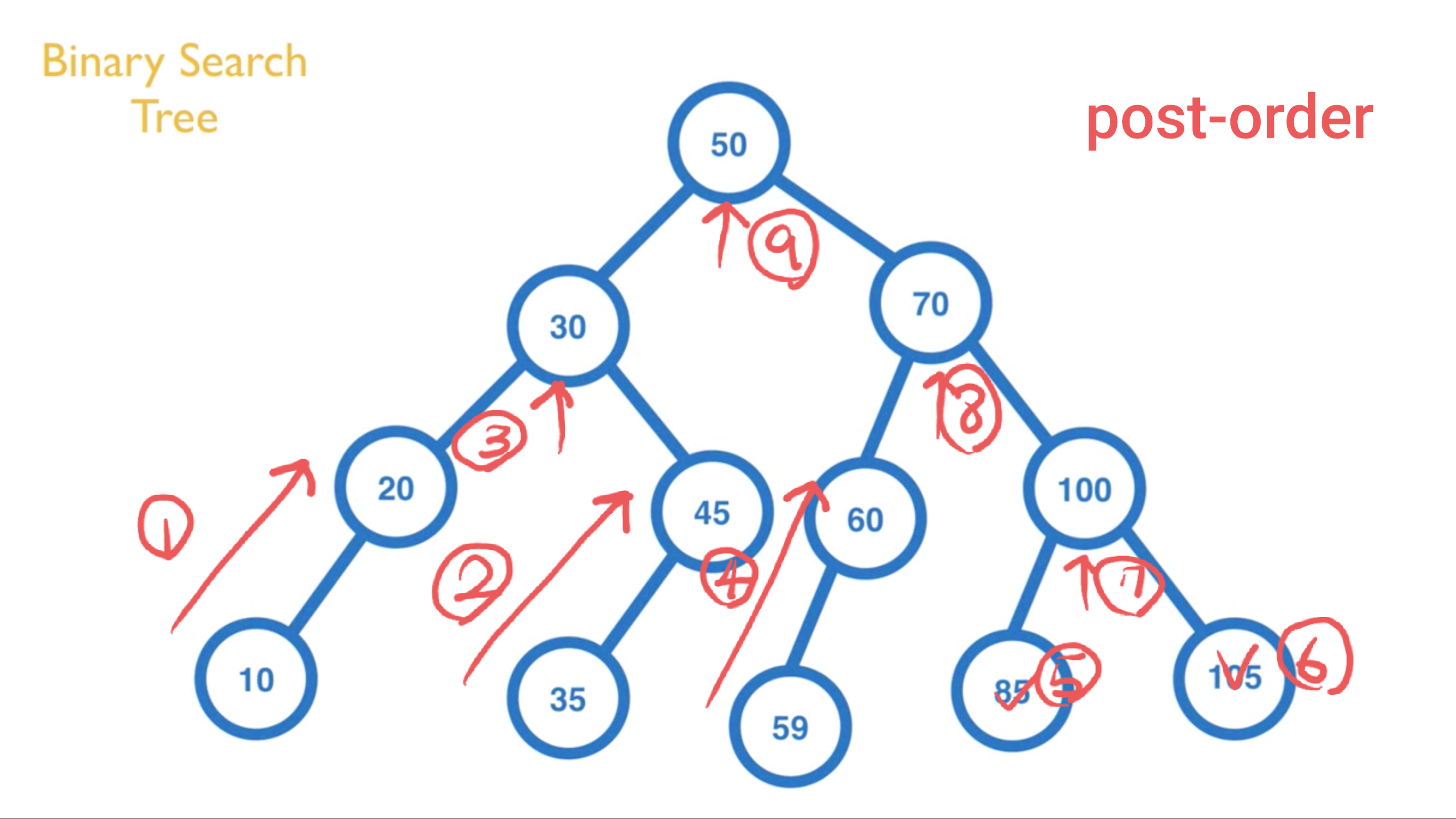
Post-Order:由下往上,由左至右(左右中)
適合使用在刪除節點時,由下往上,由左至右
以下圖為例,會輸出 [10, 20, 35, 45, 30, 59, 60, 85, 105, 100, 70, 50]
Breadth First Traversal
適合用在有階層性的資料,例如公司的組織架構,如此可以快速地找出管理職有誰,員工有誰等等
參考資料
Donate KJ 贊助作者喝咖啡
如果這篇文章對你有幫助的話,可以透過下面支付方式贊助作者喝咖啡,如果有什麼建議或想說的話可以贊助並留言給我
If this article has been helpful to you, you can support the author by treating them to a coffee through the payment options below. If you have any suggestions or comments, feel free to sponsor and leave a message for me!
| 方式 Method | 贊助 Donate |
| PayPal | https://paypal.me/kejyun |
| 綠界 ECPay | https://p.ecpay.com.tw/AC218F1 |
| 歐付寶 OPay | https://payment.opay.tw/Broadcaster/Donate/BD2BD896029F2155041C8C8FAED3A6F8 |
